知ることができる。散乱振幅F(q) は、数学的には電子密度ρ(x) のフーリエ変換になっている。 4ミラー指数 結晶面の指数 括弧の定義 六方晶の場合 Title PowerPoint プレゼンテーション Author Yoichi Nabetani Last modified by nabetani Created Date AM Document presentation format 画面に合わせる (43) Company University of Yamanashi Other titles Times New Roman MS Pゴシック Arial Calibri Symbol 標準デザイン Microsoft 六方晶の面を表す時にミラー指数でお馴染みの(hklm)について どうもh k = iという関係が成り立つみたいです。 ミラー指数については分かるのですが、何故この式が成り立つのか
ミラー指数 面 物理のかぎしっぽ
六方晶 ミラー指数 変換
六方晶 ミラー指数 変換-六方晶,非対称極点図ODF解析の注意点 対称極点図 非対称極点図(極点データの回転方向に依存する) 2.3 指数<->4指数変換 3.3指数<->4指数変換とX軸の関係をHexaConvertソフトウエアで確認 4.LaboTexとTexToolsで対称極点図を非対称ODF解析 4.1 LaboTex(A-TypeでExport)解析 4.2 TexTool 六方結晶の場合は(0001)というような表し方ですね。 いわゆるc軸が4桁目になります。(h,k,l,m)の場合、h k = l の関係があります。 参考URLに出典例を書きましたが、"ミラー指数" "0001"で検索すると、関連ページが56件ありました。




完了しました 六方晶 ミラー指数 3桁 六方晶 ミラー指数 3桁 Mbaheblogjpeuzg
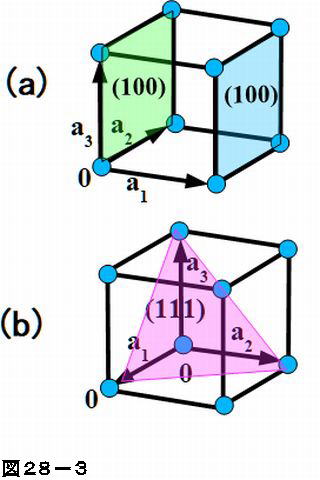
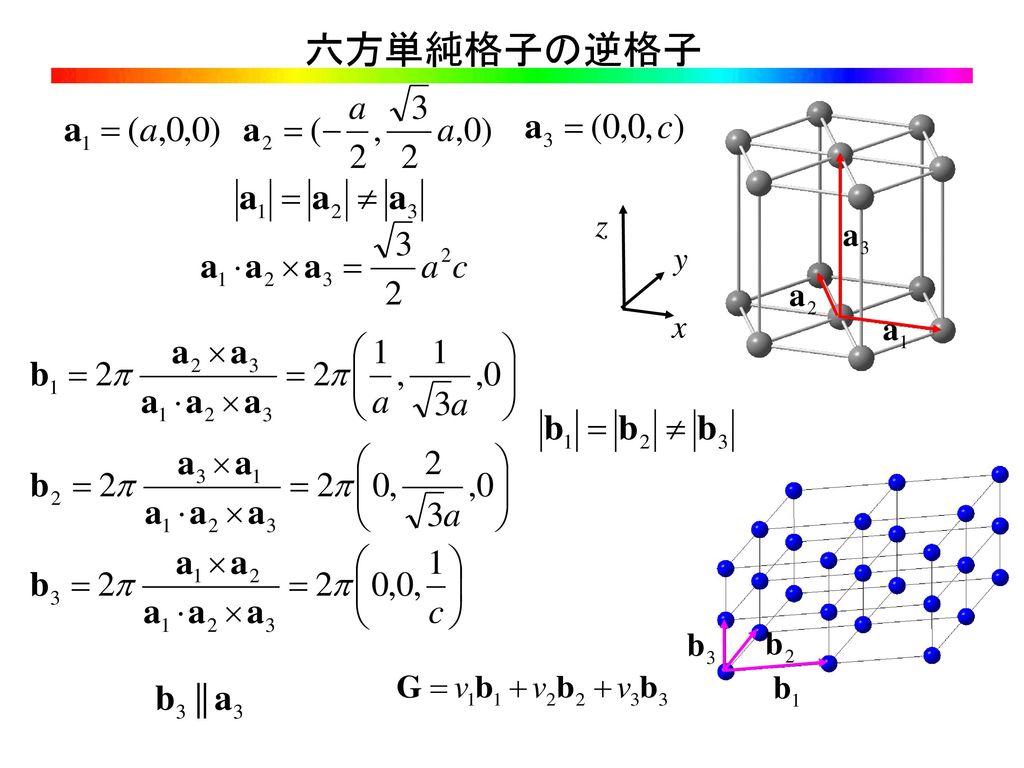
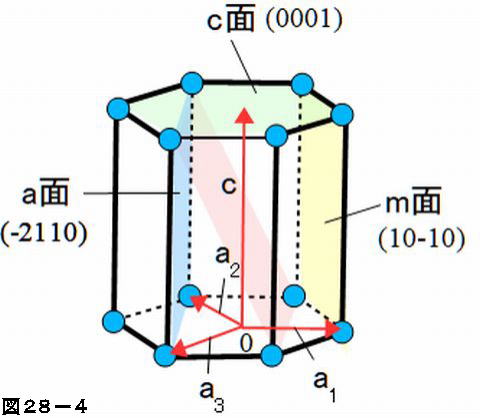
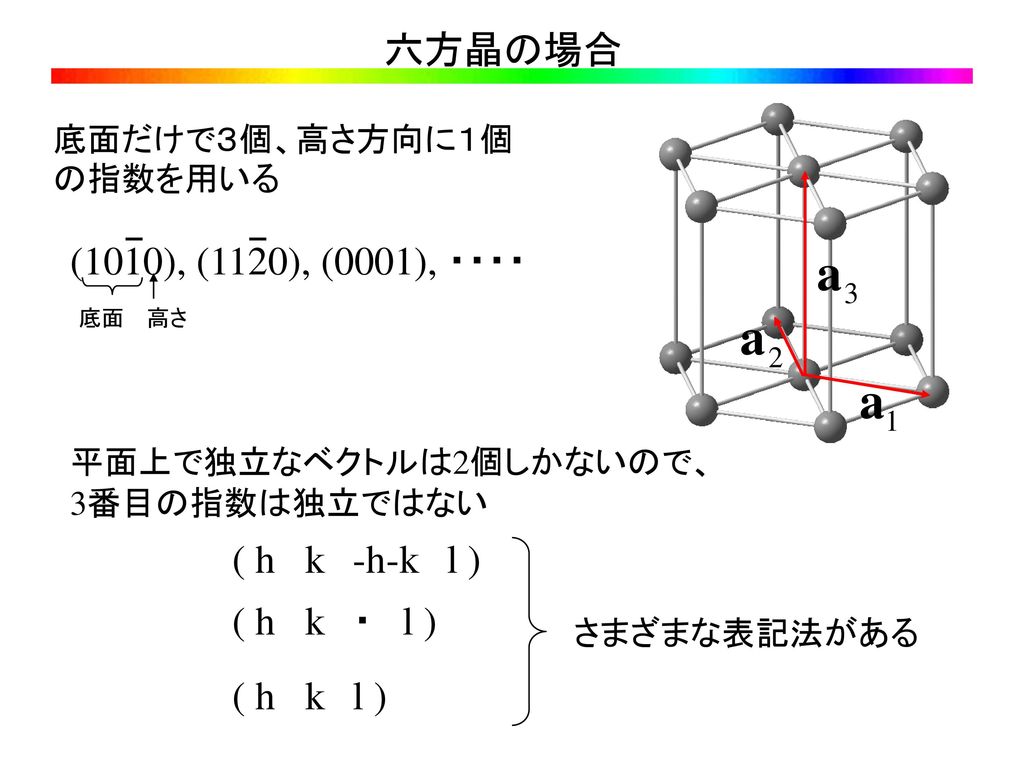
単斜晶 直方晶 菱面体晶 正方晶 六方晶 立方晶 a ≠ b, b ≠ c, c ≠ a a ≠ b, b ≠ c, c ≠ a a ≠ b, b ≠ c, c ≠ a a = b = c a = b ≠ c a = b = c α ≠ β, β ≠ γ, γ ≠ α いずれも90°ではない α = β = 90° ≠ γ すべて直角 α = β = γ (ただし、60°, 90°, °ではない) すべて直角図は六方晶を示したものである。 ミラー指数 (h k j l) をもつ格子面の面間隔を求めよ。 六方晶の格子ベクトルは 逆格子ベクトルは c a x y O A a A ミラー指数 (h k j l) をもつ格子面に対応する逆格子は で六方晶の場合 a 1 a 2 a 3 底面だけで3個、高さ方向に1個 の指数を用いる (1010), (11), (0001), ・・・・ 底面 高さ 平面上で独立なベクトルは2個しかないので、 3番目の指数は独立ではない ( hkhkl ) ( hk・l ) ( hkl ) さまざまな表記法がある
Fourier 変換 f x L f x( ) ( ) 六方格子 hex X D L S D L S D S L 記号:対称性の高い点 表面上の点:ローマ字 内部の点:ギリシャ文字 いずれも大文字 613 回析実験 未知の構造の決定や構造パラメータの正確な測定 回析過程が固体の原子構造の周期的性質に最も敏感 線源 試料 検出器 線源 :X線 電子線11 結晶系(crystal system)その2 (a=b= c, α=β=γ=π/2) (a=b≠c, α=β=π/2, γ= 2π/3) (a=b= c, α=β=γ≠π/2) 六方晶系(hexagonal system) 三方晶系(trigonal system) 体心立方格子 面心立方格子 最密六方格子 (a=b≠c, α=β=γ=π/2) 正方晶系(tetragonal system) 立方晶系(cubic system) ブラベー格子 基本単位格子 12エネルギー・ 1 Ry = eV ・ 1 eV = kJ/mol = e19 J = cm1 ・ 1 cal = 4184 J ・ 1 cm1 = E4 eV 長さ ・ 1 au(bohr) = A 超越数 ・ e = ・ pi = 物理定数 ・ k = e23 J/K = e6 eV/K (Boltzmann const) ・ N = e23 /mol (Avogadro const) ・ R = 1451 J/molK (Gas const) ・ e =
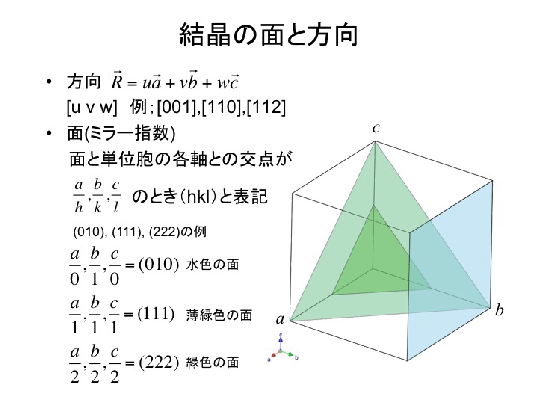
A = b = c,α=β=γ=90° ⇨立方晶 a ≠b = c,α=β=γ=90° ⇨正方晶 単位格子:3つの長さ(a, b, c) と3つの角度(α,β,γ)で規定される 原点 a ≠b≠c,α=β=γ=90° ⇨斜方晶 a b c x,y,z座標軸を描く ときは立方晶の場合、dとaの関係はミラー指数(hkl)を使って 1 d2 = h2k2l2 a2 (3) となる(課題4)。ちなみに、六方最密充填構造(Hexagonal closepacked)の場合は 1 d2 = 4 3 h2hkk2 a2 ⎛ ⎝⎜ ⎞ ⎠⎟ l2 c2 (4) と表される。それぞれの構造を持つ単位格子の体積を求めた上で、底六方最密格子の単位格子の見方と体積の求め方の説明です。 単位格子とは結晶格子の最小単位をいうので、 普段六方最密格子と読んでいる六角柱の構造は単位格子ではありません。 また、六方最密格子問題は面心立方格子問題への変換がで



金属材料基礎講座 その24 ミラー指数の方向 ものづくりドットコム



結晶の面と方向の記述方法
単純単斜格子 底面心単斜格子 7 三斜晶 a ̸= b ̸= c ̸= ̸= 単純三斜格子 o m¨ ú¨ Ø ú¨ Ø ú¨ Simple latticeBody centered latticeFace centered latticeBase centered lattice 図2 格子の種類 13 格子面と面間隔 c a b 3a 2b 2c 図3 ミラー指数 単位格子の変えた。変換後の正しい単位胞を示せ。 非対称単位(Asymmetric unit) 六方晶系 唯一の6回回転軸か6回回反軸 正方晶系 唯一の4回回転軸か4回回反軸 三方晶系 唯一の3回回転軸か3回回反軸 斜方晶系 3つの互いに直交する2回回転軸か2回回反軸 単斜晶系 唯一の2回回転軸あるいは唯一の鏡面 三斜晶系で切る平面のことである(ミラー指数のこと)。 (hkl)面とそれに垂直な逆格 子ベクトル K hkl 前ページの図に示すように、 逆格子ベクトル K hkl は(h k l) 面に垂直 であること意味している。 (証明) (h k l) 面上の以下の2本のベク をベクトルを考える。 a



窒化物半導体素子



Tsujilab Mtl Kyoto U Ac Jp
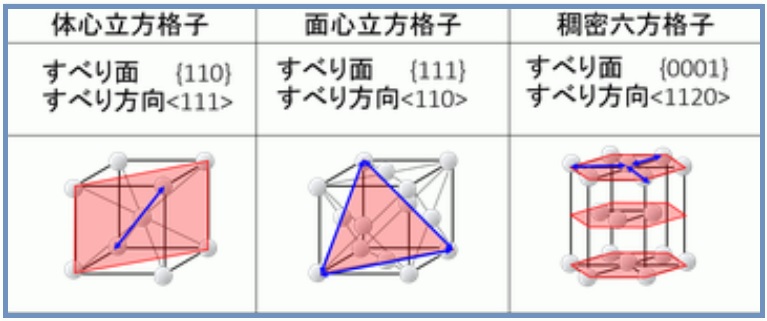
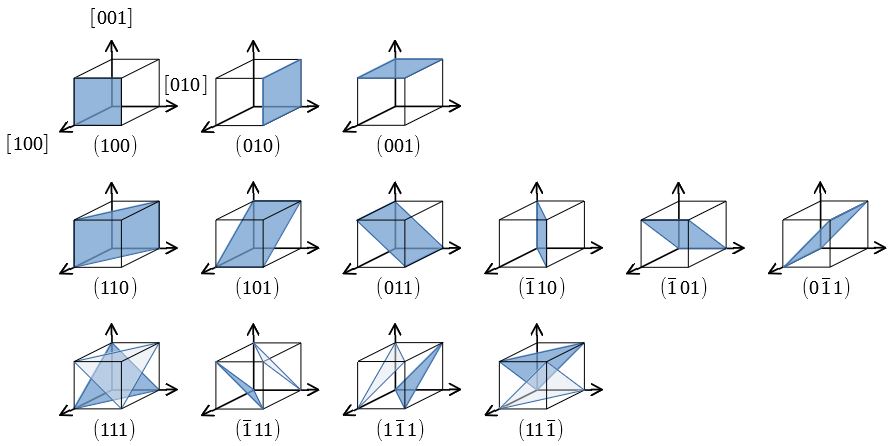
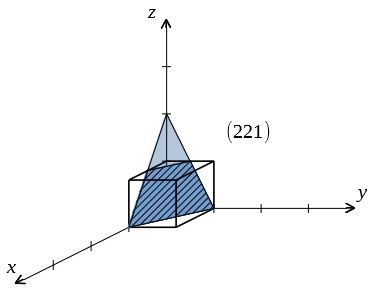
ミラー指数による立方晶・六方晶における面と方向の表し方 前回の記事では結晶の基本構造について学んだ。 金属材料の変形を結晶の観点から理解するために、もうひとつ準備をしておきたい。 それは、結晶中の面や方向を表記する方法である。 結晶は7ミラー指数 8逆格子 9回折条件 結晶構造解析i 結晶構造解析ii 結晶欠陥(転位,空孔,格子間挿入,置換) 結晶成長 立方格子 面心格子,六方格子 ブリルアンゾーン 空間群 光学モードと音響モード フォノン=場の量子化もどき ボゴリューボフ変換 2次元格子ミラー指数 463 ミラー指数の表記 < 100 > = 100,010, 001 {111} = (111),(1 11),(1 1 1),(111 ) 方向: 面:



sicエピタキシャルウエハおよびそれを用いたsic半導体素子



格子面とミラー指数の求め方
って晶 系を間違うはずがない (5)正 方晶系で(110)面 に平行なc映 進面がある時, hhl,l≠2nの 消滅則が生じる (6)三斜晶系でZ=2で あり,空間群P1を 仮定して直接 法を行ったところ解けずPlで 解けたこ れより空間 群はP1である (7)複合六方格子のラウエ群は3か3mlで あり,31mで はあり得ない (8)複合六方晶のミラー指数(ミラー・ブラベー指数) 指数UVW→uvtwの変換が存在するが、 テキスト読んでおいてください。 面の場合ほど単純ではなく、結構ややこしい (hkl)面の間隔 8 立方晶・正方晶・直方晶・六方晶 では、比較的簡単に計算できる。 正規直交基底をもつ座標系 この面と原点の 六方晶4指数表示の高次元解釈― @aki_kuwa 氏による解説 @aki_kuwa 氏に六方晶を4指数で表示する意義について、高次元の観点で大変わかり易く解説していただきました。 高次元から4指数を見ると大変見通しがよく、広く知られるべきと思います。 より詳細に



格子面とミラー指数の求め方



半導体物理学
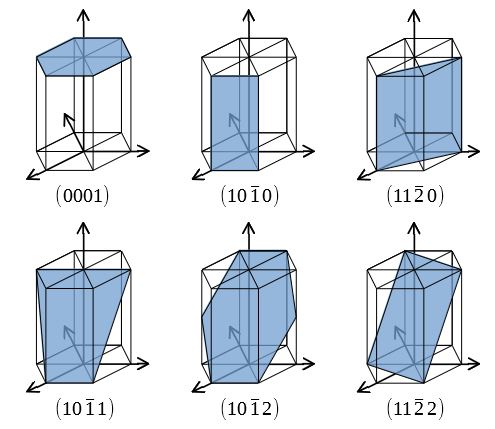
六方(ろっぽう)とは。意味や解説、類語。1 東西南北と上下との六つの方向。2 六つの平面で囲まれた立体。六面体。3 (「六法」とも書く)歌舞伎の特殊演技の一。先行芸能・祭礼行事などの歩き方を様式的に誇張・美化したもの。主に荒事の引っ込みの芸として演じられ、飛び六方・丹前 このように六方晶における等価な方位指数・面指数は,4指数記法の1~3番目の指数を循環させることで表現することができます. 一方これを3指数記法で表すと 100, 010, 110となり,等価であることがわかりにくくなってしまいます. 六方晶では c軸方位とa軸方位に即した話題がほとんどでac方位 (= {211 3}),a2c方位 (= {211 6})といった書き方もされます.4指数でミラー指数,ラウエ指数と消滅則 ロレーヌ大学 ワイスパラメーターは無限大となり,軸変換などの計算 の場合は∞という指数は扱いにくい. 上記の問題は文政8年(15年)にウィリアム・ヒュー ウェルによって解決された6)そして,ヒューウェルの表記 法は天保10年(19年)に



ミラー指数 Monozukuri Hitozukuri 日本のものづくり



Tsujilab Mtl Kyoto U Ac Jp
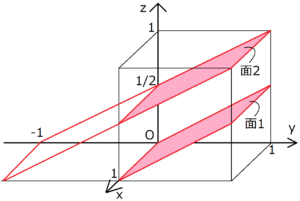
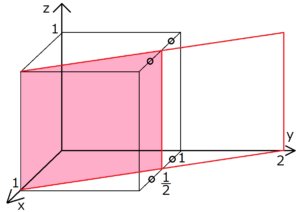
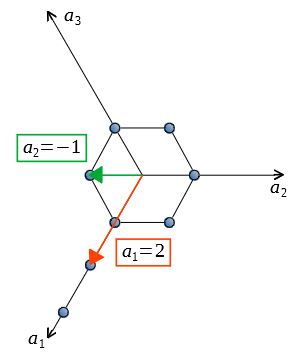
六方晶 ミラー指数 3桁低温における単斜晶の格子定数は以下の方法により求め た.格子面間隔と格子定数との関係はミラー指数を用いた式 によって関係付けられる.そこで,格子定数a m,b m,c m, b を 求めるため,4 つのミラー指数(040), (022), (2), (211˜ )に 対する格子面間隔d 1~d= 1 単純六方格子 6 単斜晶 a ̸= b ̸= c = = 90; 合わせh, k, l を面のミラー指数といい,この面に平行で等間隔な面の集合を (h k l) と表す.ただし六方晶では – (h k) = i とおいて,(h k i l) と表す 図15 いろいろな面のミラー指数 右の面はa, b, c 軸と1a, 2b, 3c で交わる.



ミラー指数による立方晶 六方晶における面と方向の表し方



ミラー指数による立方晶 六方晶における面と方向の表し方
六方晶の結晶の例として、AlN, GaN, InNのいくつか代表的な面について計算した結果を示します。 格子定数 AlN GaN InN 311 319 354 498 519 570 格子面 (001) (002) (004) (110) (102) Appendix 逆格子ベクトルが 面に垂直であることの証明 逆格子ベクトル が 面に垂直であることを示します。 面上の2つの解法(a) (・3)式に格子定数とミラー指数を代入する. (b) {399}面のミラー指数は{133}面の3倍である.したがって 面間隔は1/3である. 答.0063nm 0190nm 2767 075 3 094 3 0 1 1 2 2 2 2 2 2 2 2 = ∴ = = = d d d 答.019nm5 六方晶 a = b ̸= c = = 90;




ミラー指数 Wikiwand



Metal2 Mat Usp Ac Jp
まさしく逆空間を直接観測していることになる。フーリエ変換さえできれば、実空間構 造f(r) から回折像jF(q)j2 を予想することができるし、回折像jF(q)j2 から実空間構造f(r) を推定することもできる。 入射波 散乱波 O r kf ki 図57 位置r の点からの散乱波は、座標原点からの散乱波より、位相がϕ122 ミラー指数 結晶内の方向や面における構造の異方性を考えるためにミラー指数が用いられる.格子 面が(a b c)軸上で切る点(x y z)に対し,ミラー指数は(1/x 1/y 1/z)で定まる. 図13にミラー指数で表される面を示した.図13(a)は(111)面を示した.(x y六方晶系の面指数 a b d a b c a b d c, , , , , o を用いる (h k l) → (h k j l) A B D a h a k O a j OAB = OAD OBD 1 1 1 sin1 sin60 sin60 2 2 2 a a a a a a h k h j j k q q q h k j = 0 利点:面の対称性が明




ミラー指数 Monozukuri Hitozukuri 日本のものづくり




ミラー指数 面指数 面を示すミラー指数 4つの整数のミラー指数 と方位指数 方位を示すミラー指数 化学徒の備忘録
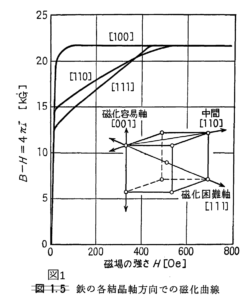
すなわち,等軸晶系,正方晶系,六方晶 系,三方晶系,斜方晶系,単斜晶系,三斜晶系である。この中で六方晶系と三方晶系は,その対称 性から,結晶面や結晶軸の方向を議論する際には必ずしも区別する必要はない。そのため,本稿で は三方晶系は六方晶系の一部として扱う。結晶軸は一般ここでは、六方晶を例にとってCohenの方法について述べる。六方晶におけるBlagg角 と格子定数およびMiller指数の関係は上に示した通りである。 いま、 λ2 3a2 = A (5) λ2 4c2 = B (6) h2 hk k2 = x (7) l2 = y (8) sin2 θ = z (9) とすれば、 z = Ax+By (10) となる。 ミラー指数と結晶面 面を示すミラー指数:面指数 4つの整数の組のミラー指数(三方晶・六方晶) 方位を示すミラー指数:方位指数 ミラー指数と括弧 ミラー指数と結晶面 結晶では、結晶面によって原子の配置が異なる。そのため、結晶面によってポテンシャルエネルギーの空間分布が異なる。




ミラー指数 Wikipedia



前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download
斜方晶(Orthorhombic)、六方晶(Hexagonal)、菱面体晶(Rhombohedra 三方晶, Trigonal)、 単斜晶(Monoclinic)、三斜晶(Triclinic)の7 種類があります。図21 はBravais 格子ですが、 さらに分類して14 種類になっています。実際にはさらに細かく分類(0 種以上)した空間 群が使われています。詳しくは、International Tables forミラー指数 ミラー指数の表記 < 100>=100,010,001 { 111}=(111),(1 11),(11 1),(111) 方向: 面:六方晶系の面指数 を用いる (h k l) # (h k j l) A B D O OAB = OAD OBD h k j = 0 利点:面の対称性が明らかになる この2つの面が等価であることがわかる



Tsujilab Mtl Kyoto U Ac Jp



ダイヤモンド構造
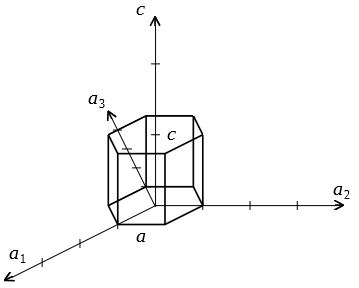
機能材料組織学 第 7 回 前回: ・すべり系 ・ミラー指数 ・ミラー指数の一括表示 今回: ・ミラー・ブラベー指数 ・分解せん断応力 ・単結晶の降伏応力 「機能材料組織学」第 7 回 71 ミラー・ブラベー指数 ・六方晶の場合: 図 71 六方晶の単位格子 方向の表示法 図 72 ミラー・ブラベー指数332六方格子のミラー指数 図312六方格子のミラー指数 立方格子との相違→a1,a2,a3,c の4軸を考える点 a1,a2,c 軸をα,β,δで横切る面 a/α :a/β :c/δの最小の整数比h:k:m を求める. 次に最後の指標をl=(hk) のように決める.



ミラー指数について質問です 六方晶の方位 12 13 が写真のようにな Yahoo 知恵袋



どちらか 生物学 息を切らして ミラー指数 波数ベクトル 結晶軸 Mitsuno Momo Jp




Wo14 号 窒化物半導体発光装置 Astamuse



Akitsu Ee Ehime U Ac Jp



ミラー指数とは コトバンク
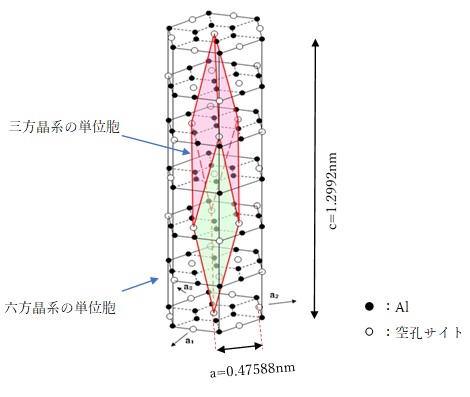



サファイアの物理的特性 株式会社 信光社




07 号 窒化物半導体素子 Astamuse



Metal2 Mat Usp Ac Jp



Acbio2 Acbio U Fukui Ac Jp




ミラー指数による立方晶 六方晶における面と方向の表し方
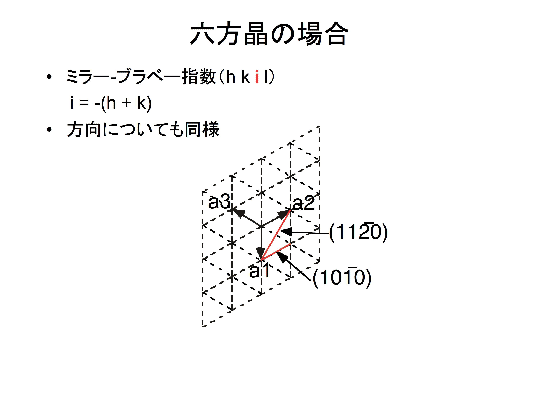



結晶の面と方向の記述方法




六方晶 ミラー指数 Ramenhuhu Com Crystal Miller I 六 物理学 教えて Goo
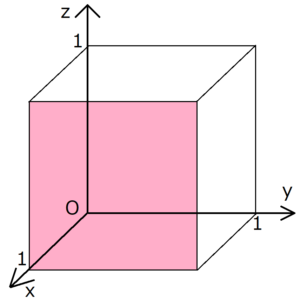



格子面とミラー指数の求め方



Akitsu Ee Ehime U Ac Jp



ときわ台学 結晶構造 ミラー指数



ときわ台学 結晶構造 ミラー指数




Wo14 号 半導体発光装置 Astamuse




ミラー指数 方向 2710 ミラー指数 方向 角度 Mbaheblogjpnmry



半導体物理 結晶構造 3 ミラー指数 Sciencompass



ミラー指数 面 物理のかぎしっぽ



モデラ Advance Nanolabo ドキュメント



Tsujilab Mtl Kyoto U Ac Jp



ミラー指数 面 物理のかぎしっぽ
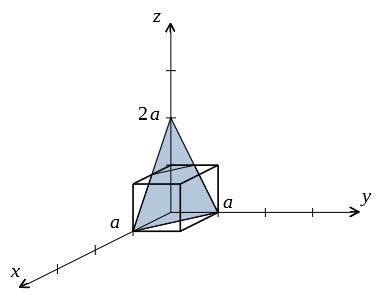



ミラー指数による立方晶 六方晶における面と方向の表し方



Tsujilab Mtl Kyoto U Ac Jp



1



Metal2 Mat Usp Ac Jp



ときわ台学 結晶構造 ミラー指数
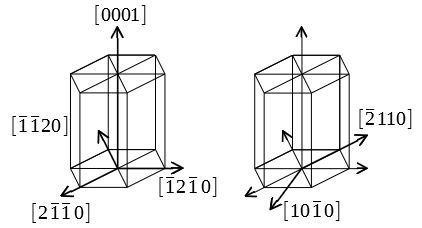



ミラー指数による立方晶 六方晶における面と方向の表し方



六方晶4指数表示の高次元解釈 Aki Kuwa 氏による解説 Togetter



ミラー指数 方向 2710 ミラー指数 方向 角度 Mbaheblogjpnmry




08 号 窒化物半導体素子 Astamuse



Tsujilab Mtl Kyoto U Ac Jp




09 号 zno系半導体素子 Astamuse



六方晶のミラー指数について質問です 下の画像の Hkil のlの部 Yahoo 知恵袋




専門 講義 結晶構造について 大学生 専門学校生 社会人 工学のノート Clearnote




Wo10 号 窒化物系半導体素子およびその製造方法 Astamuse
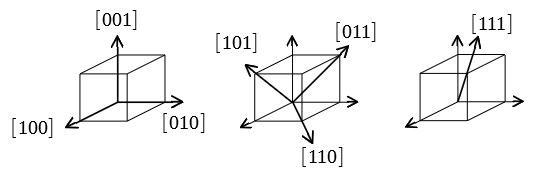



ミラー指数による立方晶 六方晶における面と方向の表し方



sicエピタキシャルウエハおよびそれを用いたsic半導体素子



ミラー指数について質問です 六方晶の方位 12 13 が写真のようにな Yahoo 知恵袋



半導体物理学



半導体物理 結晶構造 3 ミラー指数 Sciencompass




08 号 窒化物半導体 Astamuse




ミラー指数 Monozukuri Hitozukuri 日本のものづくり



ミラー指数による立方晶 六方晶における面と方向の表し方



Lab Kochi Tech Ac Jp



六方晶のミラー指数 六方晶のミラー指数の考え方はわかってる Yahoo 知恵袋



Ist Ksc Kwansei Ac Jp



Mukiken Eng Niigata U Ac Jp




ミラー指数 方向 2710 ミラー指数 方向 角度 Mbaheblogjpnmry




ミラー指数 Monozukuri Hitozukuri 日本のものづくり




完了しました 六方晶 ミラー指数 3桁 六方晶 ミラー指数 3桁 Mbaheblogjpeuzg



Tsujilab Mtl Kyoto U Ac Jp



ミラー指数による立方晶 六方晶における面と方向の表し方



ミラー指数 方向 2710 ミラー指数 方向 角度 Mbaheblogjpnmry



ミラー指数による立方晶 六方晶における面と方向の表し方
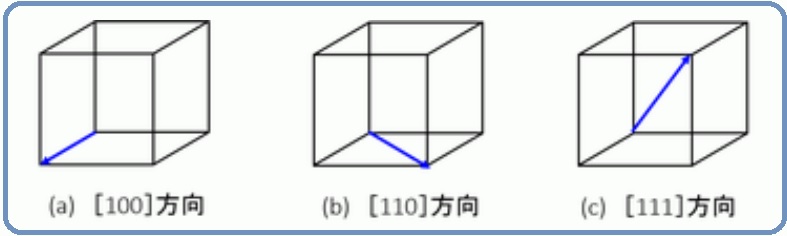



金属材料基礎講座 その24 ミラー指数の方向 ものづくりドットコム



Mukiken Eng Niigata U Ac Jp



Tsujilab Mtl Kyoto U Ac Jp




ミラー指数について




ミラー指数 Monozukuri Hitozukuri 日本のものづくり
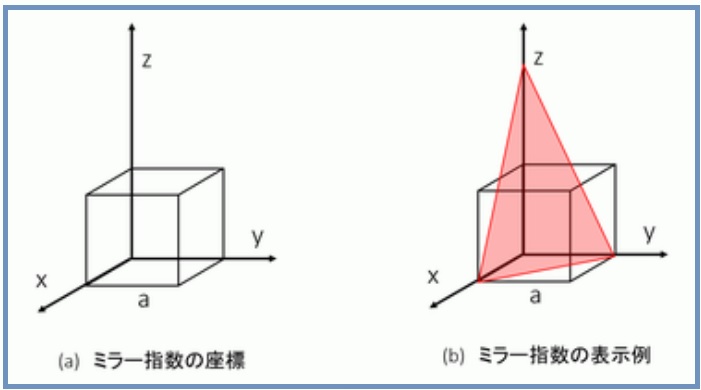



金属材料基礎講座 その23 ミラー指数とは ものづくりドットコム



六方晶のミラー指数について質問です 下の画像の Hkil のlの部 Yahoo 知恵袋



六方晶4指数表示の高次元解釈 Aki Kuwa 氏による解説 Togetter



半導体物理 結晶構造 3 ミラー指数 Sciencompass



前回の内容 結晶工学特論 第3回目 格子歪 結晶の歪 歪 応力 歪エネルギーの定義 不整合歪 基板と成長層の格子不整合に起因する歪 Ppt Download



ときわ台学 結晶構造 ミラー指数




ミラー指数 Monozukuri Hitozukuri 日本のものづくり



ミラー指数による立方晶 六方晶における面と方向の表し方



Tsujilab Mtl Kyoto U Ac Jp
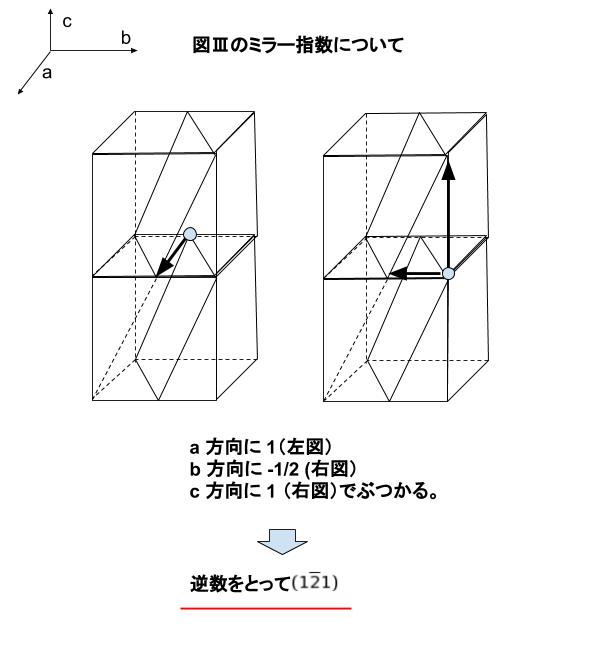



ミラー指数 方向 2710 ミラー指数 方向 角度 Mbaheblogjpnmry



sicエピタキシャルウエハおよびそれを用いたsic半導体素子



ときわ台学 結晶構造 ミラー指数



ときわ台学 結晶構造 ミラー指数



この画像のミラー指数は何かわかりますか またどのように求めたかも教 Yahoo 知恵袋



半導体物理 結晶構造 3 ミラー指数 Sciencompass



半導体物理 結晶構造 3 ミラー指数 Sciencompass
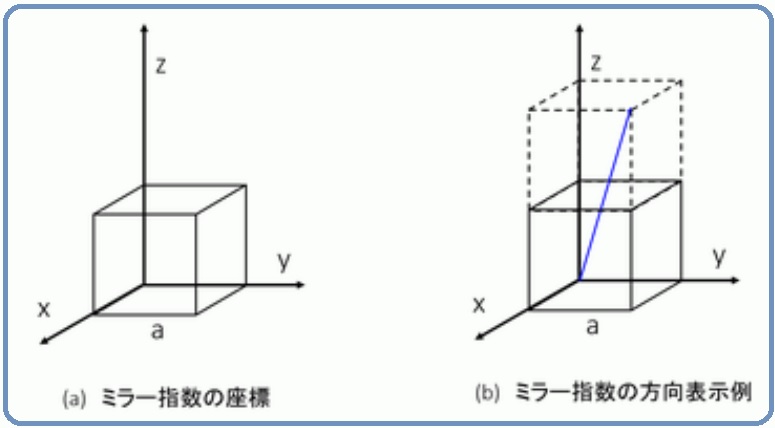



金属材料基礎講座 その24 ミラー指数の方向 ものづくりドットコム



Tsujilab Mtl Kyoto U Ac Jp



のミラー指数 方向指数 の求め方が分かりません 教えて下さい Yahoo 知恵袋



Acbio2 Acbio U Fukui Ac Jp




ミラー指数 Monozukuri Hitozukuri 日本のものづくり



0 件のコメント:
コメントを投稿